A flickr h-index, the f-index.

In science, one of the recent trends is to characterize people's careers by looking not just at number of citations and such but at what's called the Hirsch-index. The number indicates how many papers you have published that have received at least the same number of citations. So, if you have an h-number (that's where I am now) of 17, you have 17 peer-review publications that have been cited at least 17 times. The existence of this number comes from the observation that if you rank publications according to their number of times cited, you get a power-law series and the h-number basically is it's moment. Now, where does photography come in you ask? I just had an interesting observation in looking at the number of page-views my images get on flickr. If you rank them in a similar way, according to the number of image-views, it turns out that my stream has a very similar power-law behavior:


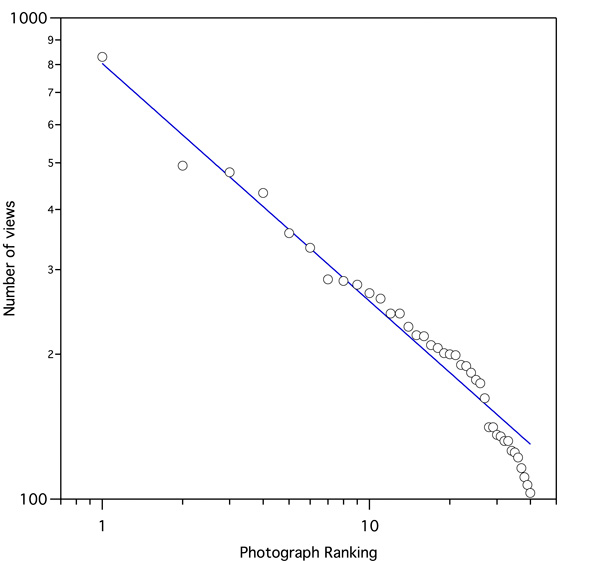
This is a powerlaw with an approximate power of -1/2. It looks remarkably similar to the distribution I get when plotting the number of citations to my scientific papers. In fact, many social phenomena are known to be distributed in a similar power-law fashion. A good example (from Murray Gell-Mann's famous book on chaos theory, the Quark and the Jaguar BTW) is the distribution of populations in US cities.
If for my flickr stream, you do the same analysis on this distribution as the h-number (on flickr you just go through your most popular sorted by views pages until you find the one where the number of views equals the ranking number) I get a f-index (instead of h-index) of 65! This is the turning point image:


What's your f-index?

My most popular flickr images

One of those interesting things about flickr is that you can check which of your images are most watched. For my flickr stream, the following 10 come out on top:

	#1: Boulder and Blue Lake • 830 views
	#2: It's alive! • 493 views
	#3: Dawn at the tip of White Crack at Canyonlands National Park • 477 views
	#4: Precipice • 433 views
	#5: Dune clouds over the front range • 357 views
	#6: Lake Haiyaha in the mist • 332 views
	#7: sunset 11/20/06 • 286 views
	#8: Blue Lake reflection • 284 views
	#9: workflow • 279 views
	#10: Rushing into the sunset • 268 views

What I find interesting about this list is that #9 is an image I put up for this blog and whose only way of being viewed is people clicking on it on the blog. That's great and must mean it is being read. It is probably just because it is a post about lightroom ;). Also interesting is that the most popular image (also the most favorited) is made using my old film camera. Strangely in the interestingness series, different photographs show up than in the most viewed or most favorited series.

Great tip

Found an excellent tip on the Lightroom support forum on how to set defaults for your camera in ACR/Lightroom. I'll be doing that for my camera for sure as I currently apply a default to files from my camera upon import to get the color a little better!

I got spammed

It seems I got spammed on this blog on my most popular post. There were a few posts there that I had to delete (before turning on moderation) because, even though they attempted to stroke my ego, were just links to sites selling viagra and peddling pay-day loans. Oh how I hate spammers. There is a special place in hell for these people. I don't like having to turn on moderation but the volume of crap is simply too high.

Capitol Reef National Park

After Goblin Valley, we stayed at Capitol Reef National Park. An often overlooked, but absolutely gorgeous place. We camped on the campground in Fruita, which was great as it is in the middle of orchards where you can just pick fruit from the trees around you. There are deer everywhere and beautiful old structures. Anyway, I managed to get up early and take some shots on a hike up the nearby mesa. Here are a few:

Along the trail upwards:


Sunrise in the wash:


The nose:


Faces:


Boulders:


Breadcrumbs:


Treestump:


The tree:


Bat caves:


Tree on slope:

Goblin Valley State Park

We (me, my wife, and my daughter) went to camp out in several beautiful places in Utah. One of the places we stayed was Valley of the Goblins State Park. An amazingly beautiful and outerworldly place. The story on how these were formed is very interesting and this place is well worth a visit. I want to go back there when the light will be better, but the threatening storm is pretty good already. Here are a few images. Bigger versions can be found by following the flickr links:

I call this one "The sewer":


Juxtaposition of green plant and red stone:


The crowd:


Alien seashore:


Lost ball


Mushroom:


As an aside, I just love lightroom to zoom through all these images and choose some good ones.